[사고력 쑥 스토리텔링 수학] (31) 진실게임

수학의 논리 문제에서도 모순 활용
가정→조건활용→추리→결과 도출

말이나 행동의 앞뒤가 맞지 않을 때 ‘모순(矛盾)’이라고 한다. 모순은 ‘창과 방패’라는 뜻으로 중국 초나라에서 창과 방패를 파는 장사꾼의 이야기에서 유래됐다. 이 장사꾼은 말을 참 잘했다. 하루는 그가 손님들에게 “이 창은 참으로 예리하여 어떤 방패도 뚫을 수 있는 창입니다. 그리고 이 방패는 아주 견고해 어떤 창이나 칼로도 꿰뚫지 못합니다”라고 자랑했다. 잠자코 듣고 있던 한 손님이 “그럼 자네의 창으로 자네의 방패를 찌르면 어떻게 되는가”라고 묻자 장사꾼은 아무런 대답도 하지 못했다고 한다.
수학의 논리문제에서도 모순이 활용된다. 주어진 조건을 분석해 참과 거짓을 정할 때 그 가정이 모순인 상황인지 아닌지 확인하는 것은 문제해결의 열쇠가 된다. 아래 예문을 보자.

“아프리카의 어떤 부족은 항상 참말만 하는 ‘참말쟁이’와 항상 거짓말만 하는 ‘거짓말쟁이’만이 살고 있다. 그 부족의 어떤 사람이 ‘나는 참말쟁이야’라고 말했다면 이 사람은 참말쟁이일까? 거짓말쟁이일까?” 

우선 이 사람을 참말쟁이라고 가정하면 참말쟁이가 맞다. 그런데 이 사람을 거짓말쟁이라고 가정하면 거짓말을 한 셈이어서 거짓말쟁이가 된다. 즉 이 사람은 참말쟁이일 수도, 거짓말쟁이일 수도 있다. 이런 논리 문제는 가정부터 한 뒤, 각각의 조건을 충분히 활용하고 추리해 결과를 얻도록 한다. 만약 모순된 결론이 나오면 또다시 가정해 만족스러운 결과를 얻을 때까지 반복하여 해결한다.

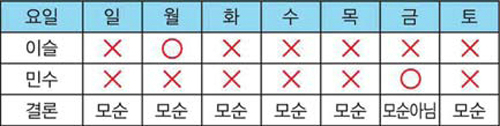
특히 논리 문제에서 두 가지 이상의 조건이 주어진 경우에는 관련 표를 모두 그린 후 조건에 따라 알 수 있는 것을 O, X로 표시하면 추론하는 데 도움이 된다. 예컨대 아래 문제를 표를 활용해 풀어보는 식이다.

민수와 이슬이는 각각 화·목·토요일과 월·수·금요일에만 거짓말을 하고 다른 요일에는 참말을 한다. 민수가 “내일은 토요일이야”라고, 이슬이가 “어제는 일요일이었어”라고 말했다면 오늘은 무슨 요일일까.

먼저 각 요일을 가정하고 민수와 이슬이가 참과 거짓 중 무엇을 말하는지 확인한 뒤, 이것이 문제에 제시된 요일별 조건과 모순인지 아닌지 판별하면 된다. 금요일만 모순이 아니므로 답은 금요일이다.

사고력수학교육기업 시매쓰출판 제공